|
反強磁性体においては,隣接するスピンは強磁性体の場合と異なり互いに反対を向こうと します.ですから,例えば簡単な正方格子のような系ではupのスピンとdownのスピンが 交互に市松模様に配置したスピン配置が一番安定となるわけです. 常磁性体のところで述べたように,その磁化率は 転移温度より十分上の高温側ではC /(T -θ) (θ < 0) に比例し, 常磁性体より若干磁化が少なく現れる系です. さて,この系の転移温度以下の磁性を強磁性体同様分子場近似(周囲のスピンを平均値で置き換える) で扱うわけですが,このとき強磁性体と異なるのはスピンを二つのグループに分けて考えるということです. なにせ,全体でスピンの平均値を取るとゼロになっちゃいますから. そこでまずupのスピンのグループをA,downのスピンのグループをBとし,それぞれの磁化を Ma,Mbとします. するとそれぞれの部分格子の感じる内部磁場は,A-B間での相互作用γ1, A-AおよびB-B間での相互作用γ2を 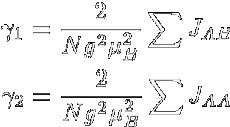 として, 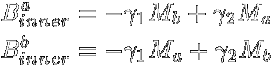 とかける.これをBrillouin関数に入れてやれば,磁化に関する式が出来上がる. さて,反強磁性で,各サイトが磁気的に(向きは反対だが)等価だとすると,部分磁化 MaとMbは等しくなる.ここでその大きさをMと置こう. すると各部分格子の磁化は以下のようにかける. 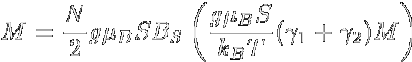 ここで頭にN/2が付いているのは,各部分格子のスピン数が全スピンの半分だからである. この式より,強磁性体のときと同様(部分格子が)自発磁化を示す転移温度 (= Néel温度,TN)が計算できて 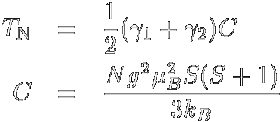 また高温側での磁化率はCurie-Weiss則に従い,そのときのWeiss温度は 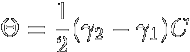 となります. さて,この反強磁性ですが,磁化の温度変化や低温での磁化過程にも特徴があります. 上記の議論では異方性はまったく考えていませんが,実際の磁性体内では多かれ少なかれ 異方性が存在します.このため個々のスピンが向きやすい方向(容易軸:easy axis)と 向きにくい方向(困難軸:hard axis)とが存在し,それらの軸間では磁化率や磁化過程が大きく異なるのです. ではまず,困難軸方向へ磁場をかけた場合の磁化過程について考えて見ます. この時,スピンの二つの副格子は容易軸から磁場B0側にθだけ傾いた方向を向きます. 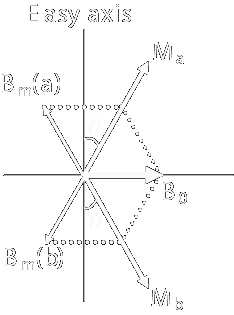 各副格子の磁化Miの向きは外部磁場と自分以外の副格子の作る内部磁場 Bmとを足した方向に向いています. この時,単純な幾何的関係から,2γMsinθ = B0が成り立ち, 外部磁場の方向には2Msinθの磁化が現れるので,この方向(困難軸)に平行に 磁場をかけたときの磁化は2Msinθ = B0/γ,磁化率は 2Msinθ/B0 = 1/γとなり,磁場に比例し温度に依存しない磁化 (= 温度に依存しない磁化率)を示します. 一方,容易軸に平行に磁場をかけた場合は,内部磁場に加えて±B0の 磁場がかかった系の磁化となる.詳細は省きます(とは言ってもBrillouin関数に代入して とくだけです) が,これは絶対零度でゼロに向かう関数となり,困難軸に磁場をかけた場合よりも小さな 磁化しか示さないこととなります. ただしこれが成り立つのは磁場が弱い部分だけで,磁場によるエネルギーがスピンの 異方性のエネルギーを上回ると,今度はスピン全体の向きが90度回転して,あたかも 容易軸と困難軸が入れ替わったかのような挙動を示します. この転移をスピンフロップ転移と呼び,この転移前後の磁化の値と磁場の強さから,スピンの 異方性の強さが求まります. 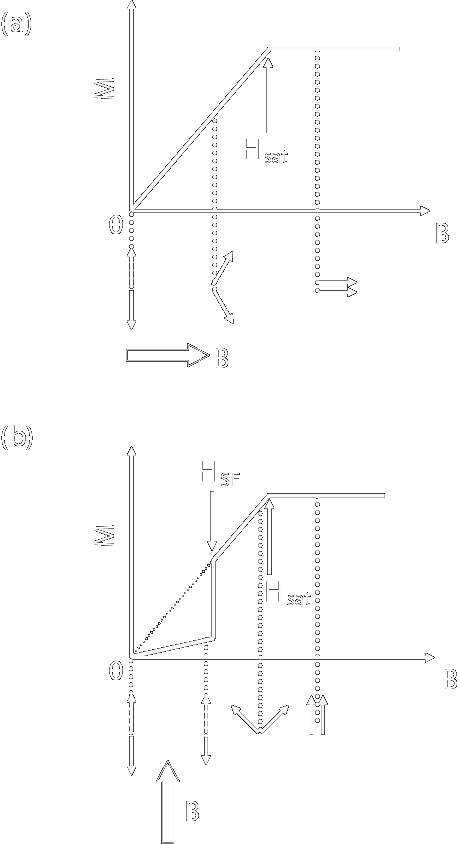 (a)困難軸および(b)容易軸に平行に磁場をかけた場合の磁化過程とスピン構造 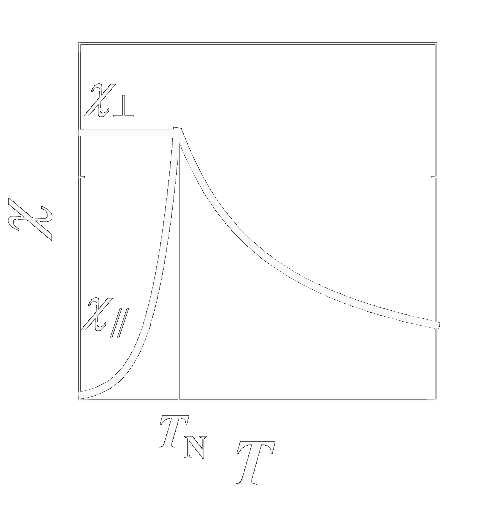 (a)困難軸(χ⊥)および(b)容易軸(χ||)に平行に磁場をかけた場合の磁化率 このため,通常の測定ではWeiss温度からおおよその相互作用の強さを,Curie定数から スピンの大きさを(HighスピンなのかLowスピンなのか,またいくつのスピンが集団として動いているのかなど), 磁化率の転移温度以下での温度変化や磁化過程の挙動から容易軸の向きを,スピンフロップから 異方性の強さを,それぞれ求めることができます. まあ,途中にいろいろな転移があったり,素直じゃない反強磁性体があったりと,そう簡単ではないことも 多々あるわけですけども. |