磁性体の測定で最もよく行われるのが，磁化の測定です．測定手段としては磁気天秤，引き抜き法及びVSM(Vibrating Sample Magnetometer)などもありますが，現在，特に微小磁化を測定する場合にはほとんどの場合でSQUID素子を利用した測定法が用いられています．
他の測定法に関してまず簡単に説明しますと，磁気天秤というのは磁性体に磁場をかけたときに生じる力を直接測定するものです．天秤に吊したサンプルに磁場をかけると，サンプルには生じた磁化と磁場勾配（磁場そのものではない）の積に比例した力が働きます．これを天秤で検出することで磁化が求まるわけです．引き抜き法はコイルの近傍においたサンプルを引き抜くと誘導電流が流れることを利用しサンプルの磁化を測定します．VSMはこの引き抜き法を振動により周期的に行うもので，検出コイル近傍でサンプルを振動させ，コイルに周期的に生じる電流（電圧）をロックインアンプで検出します．ロックインアンプで同期する成分のみを抜き出せるため単なる引き抜き法より高感度の測定が可能となります．
とまあ，こういった測定もあるわけですが，やはり分子性磁性体のような微小な磁化を測定しようと思うと，SQUID素子を用いた測定装置が感度，安定性，手軽さの面から最適です．装置としては米Quantum Design社のMPMSシリーズやPPMSシリーズが事実上の独占状態で，他社製品はまず見かけることはありません．

これらMPMSなどではどのようにして磁化を測定しているのか，と言えば，SQUID素子と呼ばれるものを測定に用いています．さらにSQUID素子を用いた測定装置には，SQUID素子としてジョセフソン結合を1つだけ含むリングを用いるrf-SQUID(radio frequency SQUID)と，2つ含んだリングを用いるdc-SQUID(direct current SQUID)の2種類が存在します．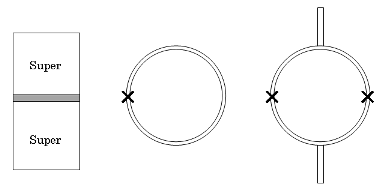
まずは簡単にジョセフソン接合の説明をしますと，これは薄い常伝導体や絶縁体を超伝導体で挟んだ構造の接合です．超伝導体の一部を非常に細くし，その部分だけ超伝導状態が壊れやすくした構造でも代用できます．この接合では挟まれた部分の厚みが非常に薄いため，両側の超伝導体から染み出してきた超伝導状態の電子の波動関数が繋がる事が出来，常伝導/絶縁性の接合を通して超伝導電流が流れることが出来ます．超伝導体で出来たリング中に1箇所このジョセフソン接合を持つのがrf-SQUID素子です．同じく超伝導リング中に2つのジョセフソン接合を持つものがdc-SQUID素子となります．

　
ジョセフソン接合の構造(左)と，rf(中央)及びdc(右) SQUID素子の構造．図中×印はジョセフソン接合を意味する．

まず最初は，rf-SQUIDを用いた測定法の原理を紹介します．まず，超伝導状態のリングを考えると，このリングをぐるっと一周回ったときに電子の波動関数の位相の変化量は2πの整数倍にならなければいけません（関数を辿ってぐるっと回っても，同じ点に戻ってきたときに関数の値は元に戻らないといけないため）．一方，磁場が存在すると，その周囲で波動関数の位相は位置による変動を示します．この両者の性質から，超伝導状態のリングにおいてはそのリングの内に存在できる磁場の量が制限を受け，ぐるっと周囲を電子が回ったときに位相変化が2nπであるような飛び飛びの値を持ちます（磁束の量子化）．さて，ここでrf-SQUID素子を考えます．rf-SQUID素子に外部磁場をかけていくと，内部の磁場がゼロである状態(2nπでn=0の状態)を保つため，リングに遮蔽電流が流れて外部磁場を打ち消します．ところが外部磁場がある値を超えると，無理に遮蔽するよりも磁束を1本リング内に入れてしまって，残りの分を遮蔽した方が安定，と言う状況になります(2nπでn=0の状態を維持するために大きな電流を流していた状態から，n=1の状態を維持するため少量の電流を流す状態へ)．この切り替わりが起こる状態近傍になるようにrf-SQUID素子に外場をかけておいて，素子の近傍においたコイルに高周波を印加すると，このコイルと電磁的に結合したrf-SQUID素子との間でエネルギーのやりとりが生じ，rf-SQUID素子の状態変化(n=0と1との間での繰り返し状態変化)へとエネルギーが吸い込まれていく共鳴状態を作れます（このエネルギーは，ジョセフソン接合部でジュール熱として放出）．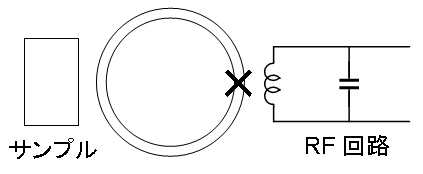

さて，この共鳴状態にあるrf-SQUIDに，ある磁化を持ったサンプルを近づけます．するとリングを貫く磁束が変化しますから，rf-SQUID素子に流れる環電流も変化，外部RF系との共鳴条件が変化します．逆に考えれば，外部RF系がrf-SQUIDと共鳴する条件がどう変化したかを検出することで，サンプルの磁化を求める事が可能になるわけです．rf-SQUIDはdc-SQUIDに比べ外乱に強く，また比較的作りやすいこともあり，早期に実用化されました．また，Quantum Design社のMPMSも，rf-SQUIDが採用されたものがかなり存在します（最近はdc-SQUIDのものもあるようです）．

続いて，dc-SQUIDの説明をします．こちらはrf-SQUIDに比べ外乱に弱いものの感度が高い，というものです．ただ最近では各種の工夫により外乱に強くなりましたし，RF発振系を使わずに単純な電圧として測定値を読めることから手軽な磁場測定機器などに用いられることがあります．dc-SQUID素子においては，二つのジョセフソン結合を持つリングに，上下に電流を流して使用します． ジョセフソン接合は，接合の上下間に臨界値以下の電流を流すとその電流値に応じた位相差θが接合の上下に生じる，と言う特徴があります(直流ジョセフソン効果．臨界電流をIcとして，I = Ic sinθ )．さてここで，dc-SQUID素子を考えましょう．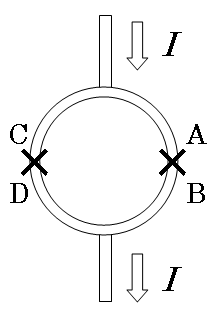

ここに，臨界電流を超える電流Iを上から下へと流します．臨界電流を超えていますので，この電流は超伝導電流として流れる成分と，ある電圧降下を伴って流れる電流の和として書くことが出来ます．そして，常伝導成分が多ければ多いほど接合部分での電圧降下は大きくなりますから，接合の上下に生じる電位差は，超伝導電流として流れる事の出来る成分の量に依存します．
では，どれだけの成分が超伝導電流として流れる事が可能なのでしょうか？ジョセフソン効果から考えると，左右の接合が等価であればそれぞれ

と書けます．ここでA，B，C，Dは図中の対応する点での位相です． 従って，このリングを上から下へと流れる事の出来る超伝導電流の最大値は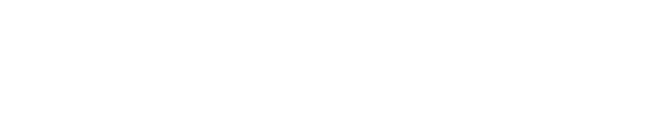

となります．さてここで，接合の下側であるB・D系と，上側であるA・C系との間にはジョセフソン接合がありますので，ここでの位相差は流れる電流値が最大となるような位相差をとる事が出来ます．そのため，超伝導電流が最大という条件下では上式がさらに変形できて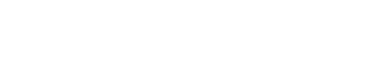

さて，ここで，B-D間やC-A間の位相差は，両者を結ぶ経路上でのベクトルポテンシャルの積分として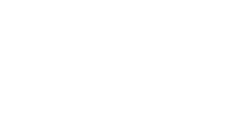

と書くことが出来ます．なお，Φ₀は磁束量子です．ここで経路B → D → C → Aを考えると，ジョセフソン接合の厚みは事実上無視できますので，上記ベクトルポテンシャルの積分2つの和はぐるっとdc-SQUID素子のリングをまとめて周回したものに等しく，それはつまりリングの囲む磁束Φに比例します（ある経路で一周ぐるっとベクトルポテンシャルを積分したものは，その経路の囲む磁束に等しい）．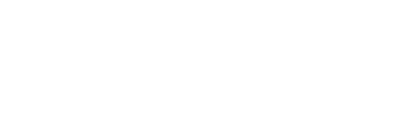

つまり

要するに，dc-SQUID素子を上下に流れる電流のうち超伝導電流の成分は，リングを貫く磁束に対し周期的に増減するわけです．これは逆に，電位差を生み出す常伝導成分も周期的に変動することを意味していますから，dc-SQUID素子の上下に生じる電位差は，外部磁束に対して周期的に増減します．つまり，ある点からの磁束の増減を電圧として検出できるわけです．

これで，rf-およびdc-SQUID素子を用いて磁化を測定する準備は整いました．しかし，実際に測定するためにはまだ大きな問題が残っています．まず，SQUID素子は非常に磁場にセンシティブなため，外部磁場等の影響を出来るだけ排除しなくてはなりません．そこでMPMSの様な装置では，SQUID素子そのものは超伝導体などによる磁気シールドの中に入れ，外部に通常の超伝導線によるピックアップコイルを出しサンプル位置まで引き出すような構造になっています．ピックアップコイル末端位置でサンプルを動かすとその磁場変動を打ち消すために電流が流れ，それがシールドされたSQUID素子直上に伝わりその場所での磁場変動を引き起こします．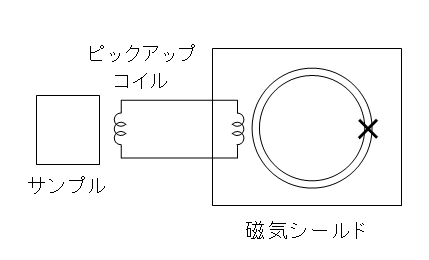

また，SQUID素子の応答は磁場に対して周期的であり，その磁場に対する応答も線形ではありません．そのためSQUID素子に対して制御された磁場をかけ，最も感度の高く応答が線形な領域に固定，そこからのわずかな差分としてサンプルの磁化を測定する方が測定上有利です．そこでフィードバックコイルを用い，あらかじめある程度の磁場をかけてSQUID素子が感度よく常に同じ応答を返す領域に持って行っておきます．サンプルの磁化が作る磁場が生じても，それをちょうど打ち消してまたSQUID素子をゼロ点に戻すような磁場をフィードバックコイルで作ってやることで，素子の最適条件を維持しつつ，その時の磁化の大きさはフィードバックコイルに流れている電流で測定できるわけです．こういった制御系をFlux Locked Loop（FLL）と呼び，精度の良い測定には欠かせません．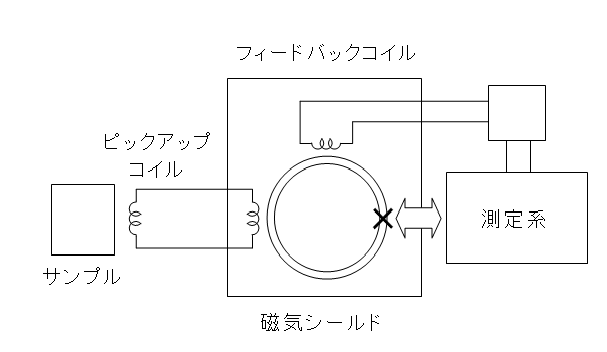

こうして検出系は構成されるわけですが，まだ問題が残ります．これはサンプル近傍での磁場を単純に拾ってしまうと，外部からの漏れ磁場の変動や，サンプルに印加している測定のための磁場の揺らぎを拾ってしまう，と言う点です．さて，このような外部からのノイズは，ピックアップコイルのごく近傍にあるサンプルを動かした際の磁場変動に比べると，遙かに遠い位置での変動になりますので，空間的な均一性はより高くなります（サンプルの作る磁場は1cm離れれば大きく異なるが，遠くの磁場源から来る磁場は1cmぐらい動いてもさして強さが変わらない）．そこで，ピックアップコイルを途中でねじることで，少し離れた場所との差分をとるように変更してやります．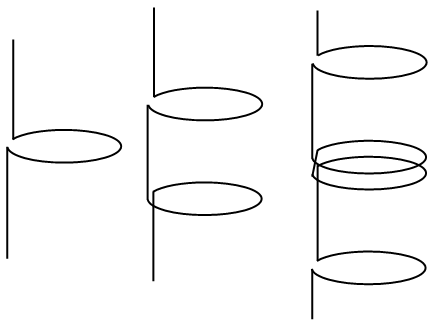

　
単純なピックアップコイル(左)と，それを改良し空間的な1次の差分(中)および2次の差分(右)を取れるようにしたピックアップコイル

右巻きと左巻きのコイルをペアにしたものは，空間的に均一な磁場変動に対して片方は順方向の，もう一方は逆方向の誘導電流を生じるため，全体としては変化が打ち消されます．このため，遠くにある磁場源からの磁場の時間変動と言ったような，空間的にほぼ均一な変化は検出せず，ピックアップコイルの位置での磁場の1次微分の時間変化をSQUID素子に伝えることが出来ます．具体的に書けば，超伝導ピックアップコイルが伝えるのは磁束の変化で，その磁束の変化は距離がdxだけ離れた二つの逆巻きコイルの位置での磁束の変化の差（逆巻きのため，効果は相殺し合う）であることから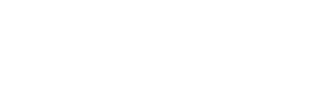

となり，近似的に磁束変化の1次微分と書けることがわかります．さらにこの1次微分型ピックアップコイルを2つ，逆向きに繋ぐと（右巻き-左巻き-左巻き-右巻き），磁場の空間方向での2次微分を取れる2次微分型ピックアップコイルが得られます．こちらも，位置xにある右巻き，x+dxにある2つの左巻き，x+2dxにある右巻き，であることから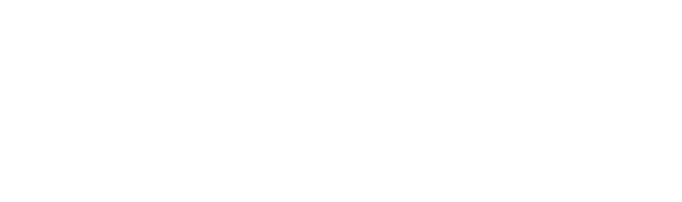

と，近似的に2次微分になっていることがわかります．MPMSなどにはこの型のピックアップコイルがセットされており，より局所的に位置による変化の大きい磁場，つまりピックアップコイルのごく近くにあるサンプルの作る磁場を選択的に抜き出せる設計となっているわけです．