|
これまで説明してきた通常の磁化率測定が静的な磁場をかけて安定状態(準安定状態) を観測するものだったのに対し,交流磁場をかけた時の応答として現れる動的な磁化を 交流磁化と呼びます. このような交流磁化はいわば電気伝導など電子のダイナミクスにおける交流依存の磁気版で, これを調べることでスピンの緩和時間等がわかるわけです. サンプルに対しある周波数f(ω = 2πf)で振幅H0の交流磁場H0sin(ωt)をかけたとします. このとき,スピンが完全にフリーであり,磁場に対し無限の応答速度で追従するならば, 磁化Mは当然M0sin(ωt)とあらわせ,磁化率M/Hは静磁場のときと一切変わりません. ところが実際にはスピンは孤立しているわけではなく,また個々のスピン自体も向きを変えるには 有限の時間が必要です.例えばスピンに異方性がある場合など,スピンが徐々に向きを変えて 行くとその途中にエネルギーの高い方向を向く瞬間がありますから,この活性化エネルギーを乗り越えられた スピンだけが反転するため,温度が下がるほどスピンの向きが変化しにくくなる,などです. このため,実際の系では観測される磁化は磁場に対し若干遅れて変化します.
この磁化は通常,ある位相だけ遅れて追従している(MAC = M0sin(ωt-δ))と表せますが,これを磁場に追従する成分(実数成分)M'と, 90度位相が遅れている成分(虚数成分・損失成分)M"とを用いて,MAC = M'sin(ωt) - M"cos(ωt)と表記します(三角関数の分解ですね). これはちょうど交流回路での電流が,理想的な抵抗によって表される部分に由来する 電圧に追従する成分と,コンデンサやコイルの存在によりかかっている電圧とは違う位相で 流れる位相のずれた成分によって,複素電流としてあらわされる(インピーダンスも複素インピーダンスになる)事と対応します.
さて,この"ずれ"ですが,スピンが自由に動ける間は当然のことながらほとんど存在しません.
一方,緩和時間が周波数fに比べあまりにも遅いときには,逆にスピンがまったく動けないわけですから
存在しない(というか交流磁化そのものがゼロになる)わけです.
逆に磁化の磁場に対する遅れが最も大きくなるのは,磁場の周波数がスピンの緩和時間の逆数に
等しくなったときで,ここから逆にスピンの緩和時間を求めることが可能になります.
とは言っても,実際には磁場を高速で振動させるのは難しいので,スピンの緩和時間が
かなり長い(=磁場の振動数が低くてよい)ような一部の系でのみ有効な手法となりますが.
このような系の例としては,スピングラス,単分子磁石,単鎖磁性体,ナノ系における超常磁性など
があげられます.
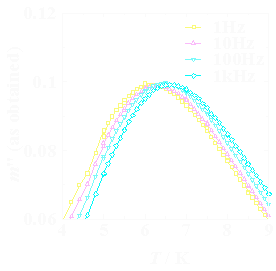 ある単鎖系磁性体(と思われる物質)の交流磁化の虚数成分M"の温度変化です. 周波数の増加とともにピーク位置が若干高温側にシフトしているのがわかるかと思います. またスピングラスでは,多くのローカルミニマが存在しそれらの間の障壁も十分高いために, 同様に顕著な周波数依存が見られます.このように,交流磁化率の測定は磁化が変化する際に ある障壁を越えないといけないような系で,その緩和時間を測定することに威力を発揮します. 一方,強磁性(フェリ磁性,弱強磁性を含む)転移の場合,転移はあくまで熱力学的にある温度で生じますから, 転移そのものには交流磁場の周波数は影響されません.このため,周波数依存を測定することによって, 単分子/単鎖磁性体のようにブロッキングにより自発磁化が現れているのか,それともバルクな 強磁性体なのかを区別することが可能です. また,強磁性体は転移温度の遥か上および下では交流磁化率が非常に小さくなります. これは転移温度よりだいぶ上では磁化が小さいこと,また十分したでは相が固定化してしまい 磁化が反転できないことに由来します.そのため,強磁性体の交流磁化M'を測定してやれば, そのピークが転移点となります.これは通常の磁化測定でFC/ZFCの一致点や残留磁化の消失点 などよりもかなりシャープに現れるので,転移温度を決定する際に便利です.
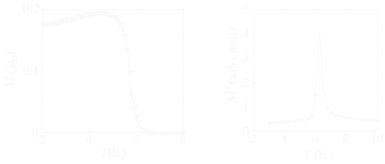 [Ni(9S3)2][Ni(bdt)2]2の残留磁化(左)と交流磁化M'(右). 交流磁化の方がかなりシャープに転移温度が現れていることが確認できる. |