相互作用
|
電子のスピンがただあるだけでは別に面白くもなんともありませんし,物質ごとの違い
なんてものも現れてはきません.
世の中に多種多様な磁性体があり,それぞれ個性的な振る舞いをするのはスピン間に相互作用が存在するためです. 1. 隣接するスピンを同じ向きにそろえようとするもの 2. 隣接するスピンを逆向きにそろえようとするもの 前者を強磁性相互作用,後者を反強磁性相互作用と呼び,実際の物質中(特に有機物や分子性磁性体) では後者のほうが実現しやすくなっております. では,それぞれの相互作用はどこから生じるのでしょうか? それを理解するには,2つの原子軌道からなる系を考えるのが一番わかりやすいかと思います. まず,二つの異なる原子上の軌道|a>と|b>があったとします.これら二つの軌道は直交はしていませんが, 第一近似として混合してより安定な軌道にはならない,とします. ここに二つの電子を入れるわけですが,簡単のため(電子間反発によって)同じ軌道に電子が 2つ入ることは無いとします.これは,2中心にそれぞれ一つずつスピンがいる状況に相当します. この仮定の下では,電子は以下の二つのいずれかの状態を取ることになります.  *実際には,さらにこれを規格化定数で割ったものになります. 二つのスピン間が同じ向きを向いたTripletの時はスピン関数は電子の交換に対し対称,一方 スピン同士が逆を向いて互いの磁性を打ち消しあうSingletの時はスピン関数は電子の交換に対し 反対称となります. フェルミオンである電子は,スピン・軌道を含めた全関数は電子の交換に対し反対称でなくてはなりませんから, Tripletでは軌道部分の関数は反対称に(=ψT),Singletの関数は対称に(=ψS)なります. さて,スピン間の相互作用を求める場合は,このψTとψS のエネルギーを比べてやります. Tripletの方がエネルギーが低ければスピンは同じ方向を向いたほうがエネルギーが低いので 強磁性相互作用,Singletの方が低ければ逆に反強磁性相互作用というわけです.エネルギーは<ψ|H|ψ>で計算できます.さて,ここでハミルトニアンを1電子に関するものと 2電子に関するものに分解します.すると1電子部分は  となります.また1電子に関する積分を以下のように置き換えておきます.  2電子に関する積分も同様に  と置きます.するとSingletとTripletのエネルギーは規格化定数も含め 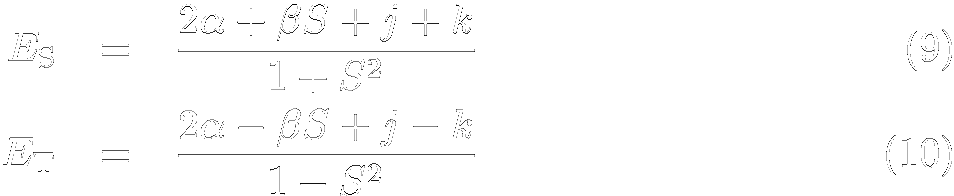 と簡単に表すことが出来ます.さて,二つのスピン間の相互作用Jは で定義されます.従って,J はSingletとTripletのエネルギー差に等しく,式(9)と(10)から計算できます. 二つの軌道の独立性が高く,S が小さい場合(通常局在スピンにはこの仮定が成り立ちます) にはS の1次の項までを取ることによって 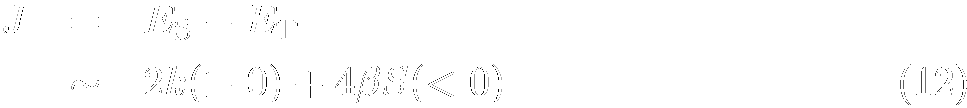 という簡単な式が得られます.これは,二つの軌道に入った電子の交換積分が大きいときは 強磁性的な相互作用が強く,一方軌道間の重なり積分や共鳴積分が大きいときには反強磁性 相互作用が強い事を示しており,特に分子性磁性体(上式が成り立つための条件であるS が小さい, を満たすことが多い)で重要な式です. 式(12)の各項が強磁性,反強磁性となることは,以下のように考えるとわかりやすいのではないでしょうか. まず強磁性となる状況は,軌道の重なりがほとんどない状況ですが,これは単一原子中の 異なる軌道の関係と同じです.この場合,複数の軌道に入っている電子はフント則から同じ向きを向く=スピン間に強磁性相互作用が働いているとみなすことが出来ます. これと全く同じ事が原子間,分子間でも起きており,その起源となっているのが交換積分なわけです. 一方,軌道の重なりが大きい場合は,二つの軌道から結合性軌道が生じ,電子は二つともそこに スピンを互いに逆向きにして入り,結合を作ります. これは電子二つからSinglet状態が生じており,電子間に強い反強磁性相互作用が働いていると みなすことが出来るわけです. 通常,分子性の磁性体では交換積分より重なり積分,共鳴積分のほうがかなり大きくなりがちなため, いかに軌道間の重なりをなくすかが強磁性相互作用発現の鍵となっています. |