|
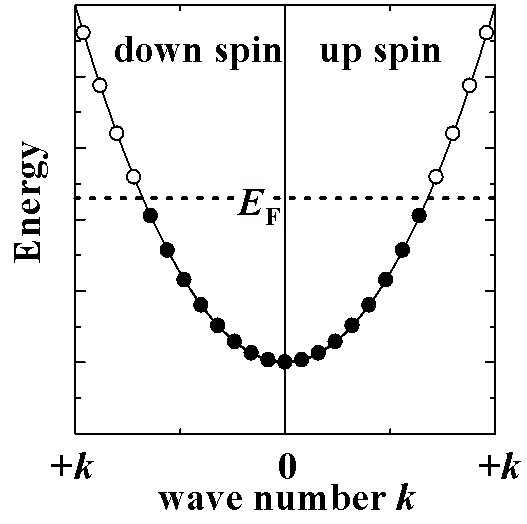
磁性にはさまざまな種類があります.まず,局在した電子からなり,単にスピン同士の相互作用で 説明できる局在磁性系,そうではなく伝導電子などのバンドからなる磁性,内核電子に由来する磁性など, 多種多様な磁性が存在します. ここでは,これらの磁性のうち代表的なものについて簡単に紹介したいと思います. 1. 局在磁性-常磁性これは局在スピンがあり,そのスピン間の相互作用が温度に比べ無視できる大きさの時に現れる磁性です. 本当に相互作用のほとんど無いような系や,強磁性体・反強磁性体の転移温度よりはるかに上の温度域 での振る舞いなどがこれに相当します. スピンの大きさS の孤立原子の取り得る磁気モーメントのz成分SZ は-S から+S までの 2S +1種類となります. *実際には角運動量L も加算されるので,J =L +S を元に考える必要がありますが,その場合も以下でのスピン角運動量を全角運動量に置き換えれば良いだけです. 各準位は磁場H のもとでエネルギーE =-g μBSzH (ここで g ,μBはそれぞれ電子スピンのg 値(〜2)およびボーア磁子)を もち,それぞれのSzの占有確率はBoltzmann分布により求まります. この場合の温度T ,磁場H の時に現れる磁化は分配関数から求まり, Brillouin関数  を用いて 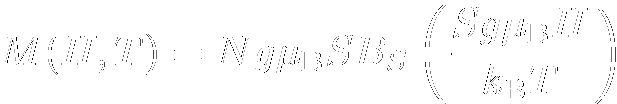 と表されます(N は孤立スピンの数,kB はボルツマン定数). この式は磁場の小さい極限で 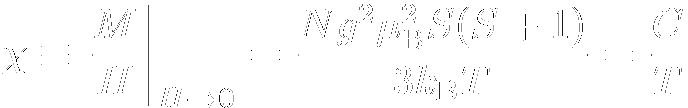 と変形されることから,相互作用の無視できる局在スピン系の磁化率は温度に反比例する ことが示せます(Curie則). 2. 局在磁性-強磁性強磁性は,次に示す反強磁性体とともに非常によく知られ,かなり昔から研究が進んでいた 磁性です. *とは言っても,身近にある磁性体のたとえば鉄などは 局在強磁性ではなくバンド強磁性ですので,強磁性の研究対象が局在強磁性の系だけだったわけではありません. スピン間の相互作用J は基本的にはJ >0で,全てのスピンが同じ方向を向いたときに 一番エネルギーが低くなります.このため強磁性相互作用は反強磁性相互作用と異なり, スピンの配置やトポロジーによるフラストレーションなどは無く,基本的にはどのようなスピン構造のものでも 素直に強磁性体へと転移します. *厳密に言えば,1次元では揺らぎの効果が大きく強磁性転移温度が0K(=ゼロ磁場,有限温度では強磁性転移はしない)ですし, 2次元でもスピンの異方性が少なくいろいろな方向を向けるHeisenberg系ではKT転移を起こし渦状になるため 強磁性体とはなりません.しかし,実際にはわずかながらも異方性があるため2次元Heisenberg強磁性系 も強磁性転移を起こしますし,擬1次元系でも低温では弱い鎖間相互作用のために転移します.  強磁性体はいったんスピンが揃うと,スピン同士が互いに向きを束縛しあってスピンの向きを固定 するため,弱い外部磁場を横向きや逆向きに印加しても強磁性体内のスピンは向きを変えることが出来ず, 同じ方向を向いたままとなります.このため,強磁性体はいったん強い外部磁場を印加しスピンの向きをそろえると, 磁場を取り去っても大きな磁化を示す(残留磁化)という,よく知られた磁石の性質を示します. しかしながら,印加する磁場の強さをだんだん強くしていくと,強磁性体内の一部のドメイン内の スピンが向きを変え始めるため,ある磁場以上では磁化の向きが反転することとなります. このときの磁場の大きさを保磁力と呼び,保磁力の大きなものを硬磁性体(Hard Magnet), 保磁力が非常に小さいものを軟磁性体(Soft Magnet)と呼んでいます. 硬磁性体はその保持する,という特性を用いてデータの保存等に,軟磁性体は外部磁場に 容易に応答するという点を生かして磁気シールドやトランスの芯などに使われています. 3. 局在磁性-反強磁性こちらは,スピン間に働く相互作用が反強磁性のものです. そのためスピンは互いに逆向きになろうとしますから,正方格子のような簡単な系だと 市松模様のようにupスピンとdownスピンが配置します.  反強磁性体は非磁性ではないので磁場をかけると磁化が現れますが,磁場中でも 出来るだけ互いが逆に向こうとしますので,磁化は非常に小さなものとなります.強磁性相互作用と反強磁性相互作用の大きな違いとして,後者においてはフラストレートが 発生する可能性がある点が挙げられます.三角格子系などのフラストレートする系では, 全ての相互作用を同時に最低エネルギーにするようなスピン配列がありえないため, スピンは中途半端な方向を向いたり,いくつものローカルミニマムを持つよになり 数多くのスピン配列が基底状態付近に存在したりと特殊な状況が実現します.  4. 内核反磁性内核で閉核構造をとっている電子は,スピンは互いに打ち消しあっていますし,軌道角運動量も 閉核構造では打ち消しあっています.では磁性はないのかと言うと,このような閉核の 電子は磁場をかけると逆向きに磁化が発生すると言う反磁性を示します. これは,古典電磁気学で閉回路に磁場をかけたときに発生する環電流によるものに対応します. 磁場がかかると,電子の軌道は元の軌道に磁場によって誘起された円運動が加算されたような ものへと変形します.p 軌道で言うならば,+1,0,-1だった角運動量が+1-δ,0-δ,-1-δへと変化するようなものです. この新たに生じた軌道運動は閉核構造を作る全電子分を足し合わせても打ち消されず残るため, 反磁性が生じることとなります. 基本的にほとんど全ての原子はこの内核電子に起因する反磁性を示しますが,不対電子があると その電子の示す常磁性や強磁性に比べ反磁性は数桁弱いため,ほとんど見えなくなってしまいます. さて,内核電子ではなくとも,結合に関与している電子も同様に軌道運動に由来する反磁性を示します. こちらは結合している原子の種類,立体構造(たとえばC-C結合であっても,直鎖なのか環状なのかで異なる) や結合次数によって反磁性の大きさが微妙に異なります. 実際の実験結果からスピンの磁化率を出すためにはこれら反磁性の大きさを見積もる 必要がありますが,その場合はパスカルの加成則が用いられます. これは物質の反磁性の大きさはその構成原子による反磁性の大きさと,結合・構造による 反磁性の大きさを単純に足し合わせたもので表せると言うもので,たとえば化学便覧などに 各原子・イオンごとの値や構造による値が列記されていますので,ここからおおよその値が 計算できます. ただ,構造に由来する部分は厳密には物質ごとに微妙に違いますので,正確な値が必要なときは同一の 構造を持つ不対電子のいない系などを測定しその値を参考にすることがあります. また,この反磁性は温度非依存の磁性です. また,芳香族化合物などは,電子がπ 軌道に沿って大きな軌道運動が可能なため,かなり大きな 反磁性磁化率を持つことがあります. 5. van Vleck常磁性電子対によって埋まった軌道を考えます.熱励起可能なぐらい低い順位に軌道があれば, これは単純なSinglet-Tripletモデル(励起した分だけが常磁性スピンとして振舞って,それ以外は非磁性)となり,ギャップのある系として温度に依存した磁性を示します. では,温度よりもだいぶ上の所に軌道があったら? この場合も,実は上の軌道が磁性に絡んできます.磁場によって軌道の直交性が若干弱まり, 上の軌道との混成軌道が基底状態となります.これにより下の軌道の軌道角運動量が例えば+1と-1だったら +1+δと-1+δへと変化し,磁場と同じ方向に磁化が生じることとなります. この混成は温度エネルギーよりも十分高い位置の軌道との混成なので,温度による影響は 無く,温度非依存の常磁性として振舞います. 6. Pauli常磁性金属中では価電子は結晶全体にわたって非局在化しています.これは分子においてπ 結合 に関与する電子がπ 系全体にわたって非局在化しているのと同じです. π 系では最低エネルギーの軌道はπ 系全体にわたって結合性の軌道でつながれた ノードのない状態で,ノードが増えるごとにエネルギーが高くなっていきます. 金属中の電子の場合も同様で,ノードがない(これを波としてみると波数k =0の波に 対応します)がエネルギーが一番低く,ノードが増える(波数が増える)ごとにエネルギーが 高くなっていくわけです.束縛が弱くて価電子が自由電子とほぼ同様に振舞える金属(アルカリ金属など) では電子のエネルギーは波数の自乗にほぼ比例します. さて,下の図を見てください.左が磁場の無いとき,右が磁場をかけたときの波数-エネルギー図 となっています(このような波数-エネルギー関係をバンドと呼びます). 各波数の状態には当然upとdownの両電子が入れますので,グラフの右半分がupの電子の 波数-エネルギー図,左半分が同downの電子のものとなっています. 磁場の無いときは,フェルミエネルギーEFのところまで状態が埋まっています(図中黒丸). up,downとも全くエネルギーは一緒ですので,upとdownの電子の数は等しく磁化はありません. ここに磁場H を印加すると,upの電子はエネルギーがg μB・1/2・H だけ下がり, 逆にdownの電子のエネルギーは同じだけ上がります(右図). 電子はEF まで埋まるわけですが,downの軌道はエネルギーが上がっているため 占有数が減り,逆にupの軌道では入る電子の数が増えています. このため,upの電子数がdownの電子数を上回り,磁化を持つようになります. このように,金属の持つバンド構造に由来して磁場をかけるとわずかな磁化が出てくる磁性を Pauli常磁性と呼びます.熱励起による占有のぼやけはup,down両者に同じように効くため このPauli常磁性には影響を与えず,温度に依存しない常磁性となります.
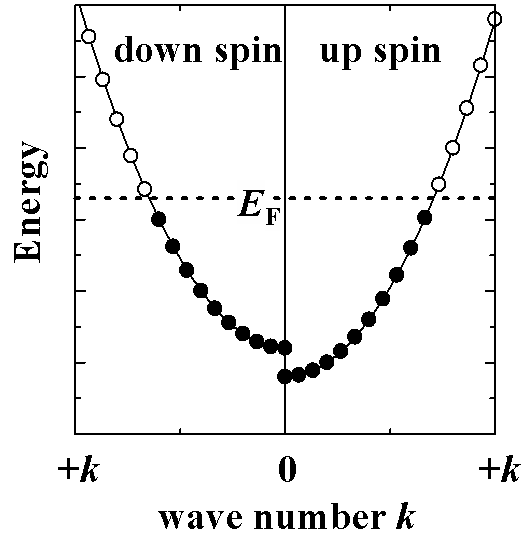
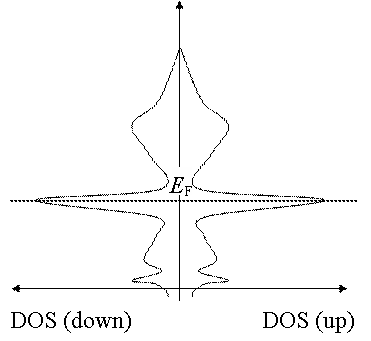
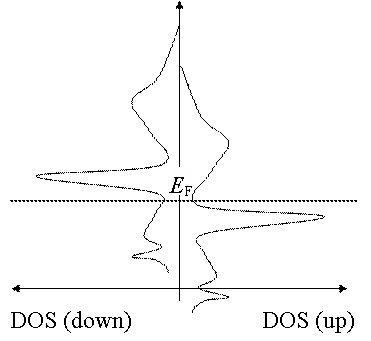
では,どの程度の常磁性が現れるのでしょうか? 磁場によるエネルギーシフトは電子の磁気モーメントによって決まっていますから, バンドのシフト量は変わりません. そのため,upとdownの電子の数の差は,EF 付近でわずかなエネルギー差の中に どのくらい準位が密に詰まっているか(=状態密度(DOS)がどのくらいあるか)に依存します. DOSが大きい場合,ちょっとのシフトで多くの準位がEF を横切って移動しますので, 出てくる磁化率は大きくなります. 逆にDOSが小さい場合,シフトでEF を横切るものがほとんど無いため upとdownの電子数はほとんど変わらず,常磁性の大きさは非常に小さな値となります. 逆に,この常磁性の大きさからDOSの大きさを見積もることも可能です. このように,Pauli常磁性の大きさはDOSに依存しますが,大抵の金属では内核の反磁性と 同程度,局在磁性よりはだいぶ小さな値となります. 例外は遷移金属やランタノイド,アクチノイドなどのd やf 軌道からなるバンドが EF の近くにある場合です.これらの軌道は互いの重なりが小さく, バンドの分散(波数が変わったときにエネルギーがどの程度変わるか.図中のグラフの傾き)が 小さくなっています.これは,分子において原子間の軌道の重なりが小さいと結合性軌道,反結合性軌道 とも元の準位とあまりエネルギーが変わらない,と言う事実に対応しています. バンドの分散が小さいと言うことは,わずかなエネルギー幅の中に多くの状態があるわけですから, 少しの磁場で大きな磁性を示すこととなります. 7. バンド強磁性Pauli常磁性のところでも述べましたが,Pauli常磁性によって生じる磁化の大きさはDOSに比例します. では,フェルミエネルギー近傍のDOSが異常に大きかったらどうなるのでしょうか? 例として,下図左に示すようなEF 付近に極端に大きなDOSのピークを持つ 金属を考えます.ここに磁場がかかると,エネルギーがupとdownで逆にシフトし,右図のようになります. さて,ここで磁場を取り去るのですが,あまりにも極端にupとdownの電子数が異なるため, 自分自身の発する磁場がこのずれたバンドをそのまま固定してしまうことがあります. これが,バンドに由来する強磁性です.
8. ランダウ反磁性これも軌道反磁性の一つで,金属中の電子が磁場により結晶中でサイクロトロン運動し,それによって生じる反磁性です. 内核電子による反磁性と基本的には同じですし,芳香族系の分子の示す反磁性と同じで分子がバルクスケールに まで大きくなったもの,と捉えてもいいかもしれません. またこのサイクロトロン運動は量子化されており,金属のバンド構造は磁場下でランダウ準位という量子化された離散的な準位へと変化していきます. |