物質の磁性は主に電子の磁性で決まり，その中でも特に局在スピンによるものが 圧倒的です． そのような局在磁性系の中でもっとも単純な系がここで示す常磁性体であり，基本的には スピン間の相互作用が無視できるような系です． この場合，S の大きさのスピンは，磁場中で2S +1個の準位に分裂し， それぞれの占有率はBoltsmann分布で求まることから，その磁化は前節で示した通り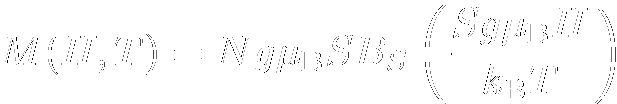

と表せます．

では，転移を引き起こさないにしても，弱い相互作用がスピン間に働く場合はどうなるでしょうか？ 相互作用が十分弱く，さらに測定時間に比べ温度が十分高い場合，隣接するスピンからの 影響は隣のスピンの磁化の統計平均値g μ_B<S >を用いて書けると考えられます．

これは，隣接するスピンの反転が十分早く 起こっていれば，その影響は隣のスピンからの影響の時間平均，つまり隣接スピンの 磁化の時間平均で書けるであろう事，また時間平均と統計平均が通常一致することによります．

あるN個のスピンからなる系に注目します．ここで，このスピン系はほぼ常磁性で弱い相互作用があるだけであり， 系全体の磁化は磁場と温度を用いてM (B ,T )と書けるとします． ここである1つのスピンに注目すると，そのスピンは隣接するn個のスピンとJ の 強さで相互作用しています．隣接スピンの平均磁化はM/Nですから， この注目している電子は常に隣接スピンからn･(-2JS <S >) = -2nJSM /g μ_BN に相当する相互作用分の影響を受けているわけです． ところでこれはS のスピンに対して2nJM /(g μ_B)²N = αM (α = 2nJ /(g μ_B)²N)の内部磁場が かかっているのと同じとみなせます． そこで，低磁場極限ではBrillouin関数が簡略化でき，自由スピンの磁化が χ = CH /T と簡略化できることを使い，このH と して外部磁場H と内部磁場αM の和がかかっているとして表すと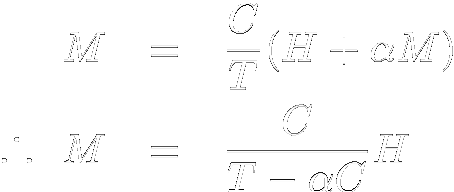

また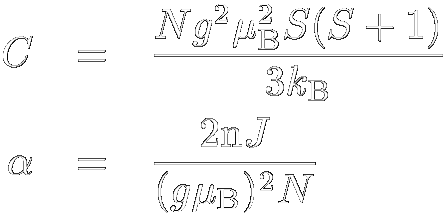

であるから，高温，弱磁場の極限では結局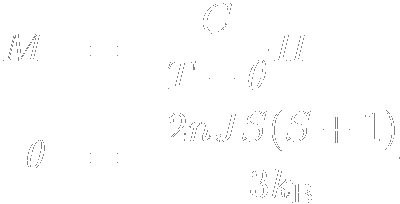