|
スピン間に十分強いJ >0の相互作用が働き,その次元性が十分高い場合などは 強磁性体に転移します. 強磁性体では,その相互作用が隣接スピンを同じ方向に向けようとすることからも判る通り, 全てのスピンが同一の方向を向いた状態になり,非常に大きな磁気モーメントが観測されます. Curie-Weiss則を導いたときと同様,周辺スピンからの相互作用をその熱平均で置き換えたもの (=分子場)で表し,強磁性について考えて見ます. まず,スピンハミルトニアンは以下のように書き直せます. 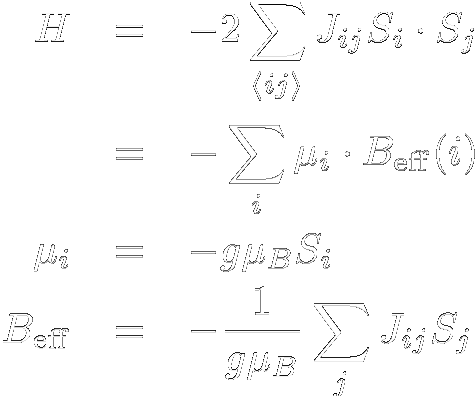 さらに,Beffをスピンの熱平均値を用いて書いてやることで 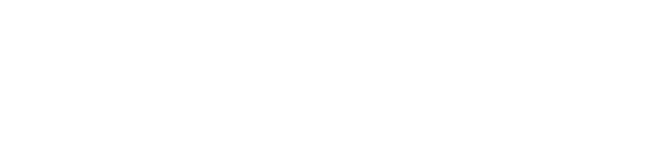 となります. ここで思い出していただきたいのは,(有効)磁場中のスピンのz成分はBrillouin関数を用いて 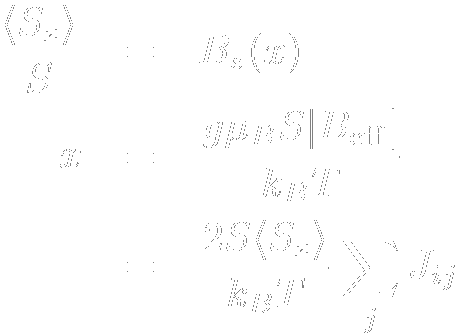 と書けるということです. これを 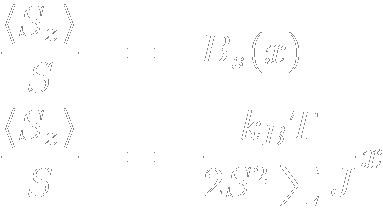 という2式のxを変数とする連立方程式と見て考えると,Brillouin関数は上に凸な関数であり, もう一式はxの1次式,つまり直線となります. 両式は必ず原点で交わりますが,後者の傾きの小さい場合,つまりT に比べS2J が 十分大きい場合には,あるxで再び両者は交わります. これは十分低温では外部磁場がなくても有限の磁化が発生する,つまり強磁性転移を示すことを 表しています. 強磁性転移を示すには(分子場近似の範囲内では)Brillouin関数の原点での傾きよりも 直線の原点での傾きが小さければよく,ここから条件として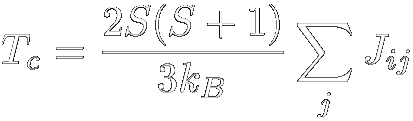 が得られ,この温度以下で自発磁化が現れることが予想されます. 強磁性体は自分自身が磁場を作るため,多少逆向きに外部磁場をかけても磁化がほとんど変化しないという 特徴があります. この時,磁化の向きを反転させるのに必要な磁場を保磁力(Coercive Force),磁場を取り去っても 残っている磁化を残留磁化(Remanent Magnetization,Remnant Magnetization)と呼びます.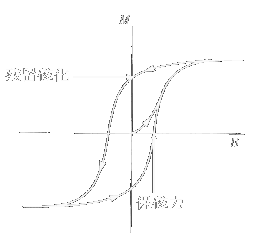 保磁力の非常に小さい磁性体は軟磁性体と呼ばれ,その磁場への追従性の良さから トランスの芯や磁気シールドに,一方保磁力の大きな磁性体は硬磁性体と呼ばれ 磁気記録用の磁性体などに用いられています. 一般に,保磁力の大きさはその磁気異方性の大きさに依存し,一軸異方性の非常に強い 系(fct格子のFePtやCoPtなど)で非常に大きな値になります. |