|
引き続きいくつかの磁性について書いていきます.
 同様に,大きさの違うスピンが交互に並んでいる(例えばS = 1のNi2+ 錯体とS = 1/2のラジカルが交互に並んだスピン鎖など)場合も,全体としてはその差分 に相当する磁化が現れます.  このようなフェリ磁性体の場合,高温では各スピンがバラバラに動くためCurie定数は 各々のCurie定数の足し合わせになりますが(例えばS=1とS=1/2からなる交互鎖の場合, Curie定数は0.375 + 1 = 1.375 emuK/mol),温度の低下と共に反強磁性近距離秩序が 発達,これは実効的にスピンを減らすため(上記の例だとS = 1-1/2 = 1/2のスピンの ように振舞うためCurie定数は0.375に近づく)低温になるほどCurie定数は小さくなります. さらに温度を下げていくと,相関長が伸び,大きなスピンとして振舞うようになる (例えばS = 1/2のラジカル10個とS = 1の錯体10個がまとまって動けば,S = (1-1/2)*10 = 5のスピンのように振舞う) ことから,今度は温度の低下と共にCurie定数は増大し,ついにはNéel温度 で磁化率は強磁性体同様発散します. フェリ磁性体の磁化過程は低磁場側では強磁性体に非常に似ているますが,そのヒステリシスループで 出てくる磁化は飽和磁化よりも小さな値となります.これは例えば上記S = 1とS = 1/2からなる 系で言えば,低磁場側ではS = 1が全て磁場方向に揃い,S = 1/2が全て逆方向に揃った状態と その反転したものとの間でヒステリシスを描くためで,さらに磁場を強くかけていくと S = 1/2のスピンが徐々に磁場方向に揃っていくことに由来する緩やかな上昇曲線を 描きます. そのため磁化過程としては反強磁性体の磁化過程に強磁性体の磁化過程を足し合わせたような形状の 曲線が得られますし,スピンフロップなどを示すこともあります.
Solid State Communications, 116 (2000) 661 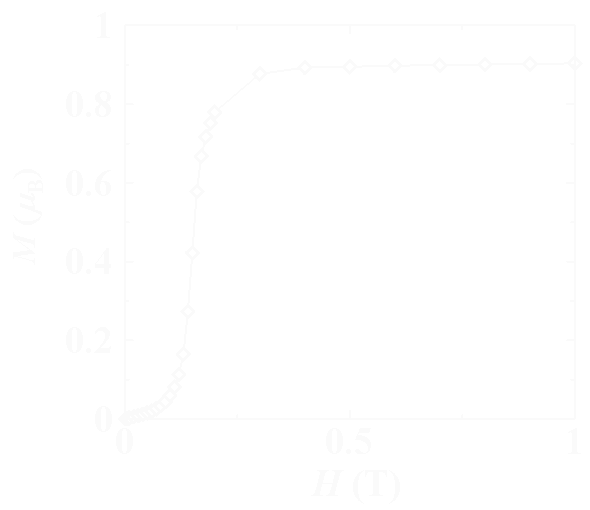 このような挙動をとる磁性体としては,主に二種類のものが挙げられます. まず第一は非常に異方性の強い磁性体.この場合スピンは特定の方向しか向けませんから, 反強磁性体に磁場を加えていくとスピン間の相互作用以上の強さの磁場がかかった瞬間 に,磁場と逆を向いていたスピンが反転して磁化が飽和することになります. この場合,容易軸に直交する方向に磁場をかけるとほとんど磁化が現れませんので, 比較的簡単に見分けがつきます. もう1つの可能性は,強磁性のものが反強磁性的に積みあがっている場合です. 例えば1次元強磁性鎖の鎖間に弱い反強磁性相互作用がある場合,鎖内ではスピンが揃い, 鎖間で逆を向くことになります.ここに磁場をかけると,鎖間の相互作用を磁場が上回った瞬間 全ての強磁性鎖の磁化が同じ方向を向くため一気に磁化が増えます. 同様に,面内相互作用が強磁性で2次元強磁性シートを作り,シート間が弱い反強磁性 の場合も,同様にある磁場で一気に磁化が増えるわけです. このような磁性体はメタ磁性体と呼ばれます.まあ,反強磁性体と言っても間違いではありませんが(実際,そう言うこともよくあります).
*鉄などの磁性金属は単体ではバンド強磁性であり 局在スピンではありませんが,希釈合金系では局在スピンを持つような事が良くあります. これは磁性金属のd軌道が金属中で欠陥(束縛ポテンシャル)として働き,そこにトラップされた 電子が局在モーメントを示すというふうに捉える事が出来ます. ただし,束縛ポテンシャルが局在化した電子を生み出すか,それとも(やや欠陥周りで 存在密度が高いけれども)非局在化した電子を生むのかは母体金属-磁性金属の組み合わせや濃度で 変わりますので,磁性金属を希釈したからといって局在モーメントが出るかどうかは 一概に言えません. 金属中の希薄な局在スピン間の相互作用は伝導電子が媒介します(RKKY相互作用). 局在電子と相互作用した伝導電子は欠陥で散乱された伝導電子と同様,その波数kで 振動する粗密波となります.例えばupの局在電子のいる軌道にdownの伝導電子が入り 相互作用することで,局在電子の周辺と,そこからkの波数に対応する距離だけ離れた場所で downの伝導電子の密度が高くなるわけです. downの電子に粗密が出来ると,upの伝導電子はその逆の粗密波となり現れます. つまり,磁性欠陥周りには波数kでup-down-up-downという伝導電子のスピンの分極が 現れてきます. さて,離れた場所にある別の磁性原子はこの分極した伝導電子と相互作用しますから, その磁性原子がup-downどちらが安定かは距離に依存することとなります.最初の磁性原子(up)の 極近傍ならdownの伝導電子が多いのでupを,ちょっと離れるとdownを,もう少し離れるとまたupと, 相互作用が空間的に振動するわけです. この結果どうなるかというと,合金中にばら撒かれた多数のスピン間に強磁性・反強磁性相互作用が 強さもいろいろでばら撒かれているような磁気構造となります. このため各所でフラストレーションが起きますし,ある部分のスピン構造をより安定に しようとすると一気に多数のスピンの向きを変えないといけない,というような状況が生じます. これはスピングラスという名前の由来であるガラスの構造を考えていただくと類似性があり分かりやすいかと思います. SiO2の最安定な構造は結晶を組んだ状態-水晶です.しかし石英ガラスでは,組成もSi原子周りの 構造も同じながら,SiO4の4面体のつながりが崩れて乱雑なものとなっています. 当然安定構造は水晶なのですが,ある一部のSiO4の4面体の向きを変えるとその周囲に歪みが生じ, よりエネルギーが高くなってしまいます.全部の4面体を同時に再配列すれば最安定構造に 落ち着けるのに,少しずつ結晶に変えていこうとすると非常にエネルギーの高い中間状態を とらなくてはいけない.そのため石英ガラスは結晶化できず乱雑なガラス構造のまま固まって しまっているわけです. これと同じように,スピングラスでも互いの相関により最安定では無いスピン構造で固まります. お互いのスピンが相互作用しあっているために,より安定な状態に動かそうとすると途中で 非常にエネルギーの高いスピン構造をとらなくてはいけない.だから動けなくなり固まっている. これがスピングラスです.また通常のガラスと同じように,ほとんど同じエネルギーを持った 配置が無数にあります.そのため,冷却の仕方(速度や磁場の強さ)により違う準安定状態に 落ち込むため,磁性において履歴を示すわけです. 最期に,スピングラスの物質が実際にどのような磁化率を示すかを軽く紹介したいと思います. まず代表的な挙動としては,磁化率の温度変化に現れるカスプがあります. 一見反強磁性体のようですが,磁化率が磁場依存し,磁場が小さいほどカスプは先鋭に,カクッと折れ曲がるような挙動を示します. またこの転移はガラス転移ですので交流磁化率においてはカスプの位置は周波数に依存し(=緩和が遅くなっていることを示す), 周波数が高いほど高温に移動します. 磁場中冷却(FC)とゼロ磁場冷却(ZFC)での磁化率が異なり,ZFCではカスプが現れるのに対し FCではガラス転移点以下においてより大きな磁化率(温度にあまり依存しないことも多い)を示します. これはFCとZFCのそれぞれの場合で落ち込んでいる準安定状態が異なるためです. 比熱においてはガラス転移温度では異常を持ちませんが,その上の温度でブロードなピークを示します. また(ガラス状態ですから)顕著な遅い緩和を示し,例えばZFCのスピングラス相を磁場中で放置することで 緩やかに違う準安定状態(FCのスピングラス相に近い)へと緩和させることが出来ます. これに関連し動的スピン緩和という面白い現象も見つかっています.例えば10Kで途中まで緩和させ, その後20K(しかし未だグラス相)に上げると前回の緩和の記憶は一旦リセットされるように見えますが,また10Kに下げると緩和が"前回の緩和の続きから"始まるというものです. 再度20Kに上げると,今度は20Kでの緩和の続きの緩和が始まります. これはあたかも各温度での緩和の状態を記憶しているようなもので,いろいろと研究が行われております. スピングラス系は統計物理の問題として面白く,発見から何十年もたっているのに未だにいろいろな点で 議論が行われている系となっています. |