|
実験的に測定できるのは磁化ですが,磁場が弱く磁化が飽和磁化に比べ十分小さいような状況では その測定された磁化を測定磁場で割ればほぼ磁化率とみなすことが出来ます. 磁化率は磁化の磁場微分∂M/∂Hのゼロ磁場極限ですが, 弱磁場領域では通常(転移点より上の)磁化は磁場にほぼ比例するので,これをM/Hで近似出来ます. まずこの磁化率の温度変化から非常に多くの情報を得る事が可能です. 1.4で示した通り,常磁性部分での磁化率の温度変化は近似的に Curie-Weiss則 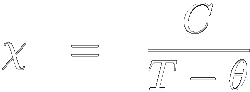 で表され,θの大きさは相互作用の強さに比例したような値となります. そこでまずχTの値をとり,温度に対してプロットしてやります.十分高温ではθに比べ Tが十分大きくなりますから,上式はχT = C/Tと簡単になり,その傾きからCurie定数, つまりスピンの大きさや数が判断できます. 続いて1/χを温度に対してプロットしてやると 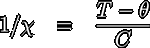 となりますから,高温側の1/χを延長した直線がゼロになる温度を用いてθを求める事が出来, ここから磁気相互作用の強さを推定する事が出来ます. 実際に相互作用の強さを求めるには,スピン間が何本の 相互作用で結ばれているのかも重要になりますので構造のデータも必要です.またいくつかの 強さの違う相互作用が存在する場合にはCurie-Weissの式のような簡単な形にはなりませんので, 構造から推定される磁気構造に基づいた計算が必要となります.
さて上記は相互作用に比べ十分温度の高い高温部分に関してでしたが,低温部分に関しても
磁化率の挙動からある程度の情報は引き出せます.
χTの値が低温に行くほど小さくなれば,これはスピンが常磁性の場合よりも磁場の方向を向きにくい
ということですから反強磁性相互作用の存在を,一方低温に行くと大きくなるなら強磁性相互作用の
存在を示しているわけです.
また一旦小さくなってより低温では発散するような傾向を示すとすると,フェリ磁性体である可能性が
高くなります.これはある程度の温度までは隣接スピン同士(例えばS=1と隣接するS=1/2)がスピンを打ち消しあって
χTが小さくなるものの,短距離秩序が発達すると今度は大きなスピンの塊
(例えば1-1/2-1-1/2-1-1/2という塊がフェリ鎖を作ると実質的にはS=3/2のスピン)として振舞うためです. 他にも,χTが高温である一定値をとり,低温でより小さな一定値に落ち着く場合には, 短距離での反強磁性の塊を作っている(例えばS=1/2の分子3つがtrimerを組んで,3分子でS=1/2の スピンとして振舞ったり,S=5/2とS=3/2の隣接分子がdimerを組んでS=1の塊として振舞ったり) とか,high spin-low spinのスピンクロスオーバーを示していると言うことも見つけられます. これとは逆に,χTの値が増えて一定となる場合もあり得ます. 例えば単分子磁石として有名なMn12は,S=3/2のMn4+が4つ, S=2のMn3+が8つからなる系です. 高温では各スピンは独立に動きますから,χTの値は1.875*4+3*8=31.5 [emu K mol-1] を示します.これに対し,十分低温ではMn4+とMn3+の間に働く 反強磁性相互作用が温度揺らぎに対し十分強くなりますから,Mn12クラスターは S=2*8-3/2*4=10と,S=10の分子として振舞い,この時のχTの値は55 [emu K mol-1] と大きくなるわけです. このように,隣接分子間や分子内などに強い相互作用が働き,他との間はそれよりかなり弱い 相互作用の場合はχTの温度変化にはっきりとその兆候が現れますので,結晶構造と合わせて スピン構造を決めるのに役立ちます. |