磁化率の温度変化と共に重要なのが，ある温度での磁化の磁場依存です． 特に転移温度以下では，この磁化過程から非常に多くの情報を引き出すことが出来ます．まず重要なのは飽和磁化です．ある程度以上の磁場で磁化が一定値になっている場合， (基本的には)全てのスピンがその磁場方向に揃っているということから，その時の 磁化の値を用いてスピン量が見積もれます．

ただし，時として磁化の途中でプラトーを持つような系がたまにあります． 強磁場をかけるとさらに大きな磁化が出るので区別可能ですが，プラトーが最大磁場の あたりだと紛らわしい？かも． 一部の量子スピン系などで出るようですが，自分の測った系では未だ出たことはありません．

強磁性体では，その異方性の強さが保磁力と残留磁化にに効いてきます． 異方性が大きければスピンの反転が起こりにくいわけですから，残留磁化も 保磁力も大きくなる傾向があります． ただ，強磁性体の場合微細なドメインのサイズが変わることで磁化が変化し得るので， ドメインウォールの動きやすさ(欠陥の過多等)などいろいろな要素がからみ， そう単純ではありませんが．

強磁性体の磁化過程．スピン源が単一種のイオンなら，飽和磁化を原子数で割れば各原子の 磁気モーメントが分かる．

このスピン量と，磁化の温度変化から求まるCurie定数を用いれば，結晶構造が分からなくても どの原子がhighスピンでどの原子がlowスピンか，などがある程度予想できます． また，磁化過程の形状はそのスピン系の基底状態の種類に大きく依存します． 先に示した強磁性体以外でも，例えば反強磁性体は磁化の立ち上がりが遅く，異方性を測れば 磁場にほぼ比例して磁化が増える困難軸2軸と，あるところで磁化過程の傾きが急に増える(スピンフロップ) 容易軸の二種類が確認できますし，らせん磁性なららせんが傘状に閉じていく1つの方向(困難軸) と，らせんの円があるところで回転する容易軸2軸が確認できます． これらの磁性体ではスピンフロップ磁場で，異方性により容易軸を向こうとする傾向と， より大きな磁化を生じて磁場に対する安定度を上げようとする傾向が釣り合っている， つまり，

• スピンフロップ前後での磁化の大きさの差とその時の磁場の強さの積(これは磁化が増えたことにより どの程度エネルギーが安定化したかを示します)
• 異方性エネルギー

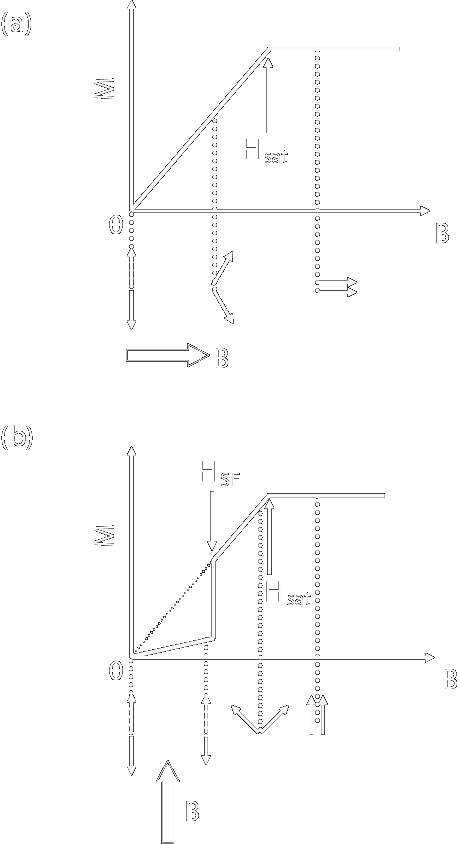反強磁性体の磁化過程

ある面内(もしくは鎖内)が強い強磁性で，面間(鎖間)が弱い反強磁性の場合はメタ磁性 を示してある磁場で急速に磁化が立ち上がる挙動が確認できます．この際，メタ転移磁場では 磁場によるエネルギーがちょうど面間(鎖間)の反強磁性相互作用を打ち消す強さを持っているわけですから， この磁場から面間(鎖間)の反強磁性相互作用の強さが決定できます．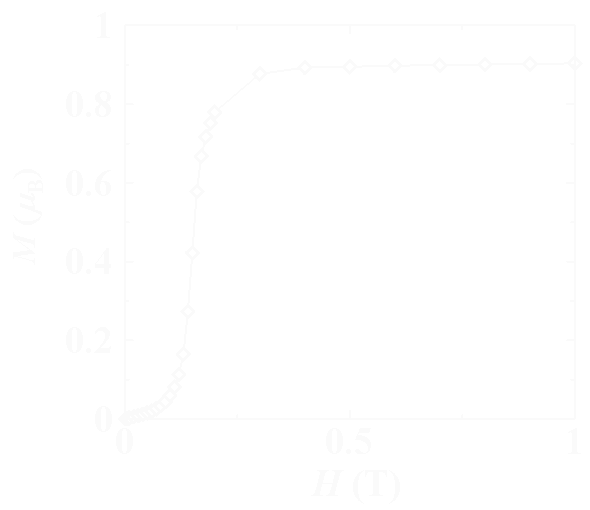

メタ磁性体の磁化過程

一見強磁性体のようだが違うと言うパターンに，フェリ磁性体があります． この場合，スピンの打ち消しきれない分が残ってきて強磁性的に振舞いますが，さらに磁場を 上げていくと磁化が緩やかに直線的に増加していきます．例えば3/2-5/2スピンが同数 並んだフェリ磁性体では正味S=1の磁化が残りますから，S=1スピンの強磁性体が 示すヒステリシスループに，残りの磁化である6μ_B分の反強磁性体の 磁化を足したような磁化過程となるわけです． 従って，スピンの大きさと量が分かっている物質なら，この時の小さめのヒステリシスループの 大きさからおおよそのスピン構造は予想できます． また類似の磁化過程を示す系として弱強磁性体がありますが，こちらは通常ヒステリシスループの 大きさが非常に小さく，全磁気モーメントの数％以下の自発磁化しか示さないことも多いため ある程度見分けはつきます．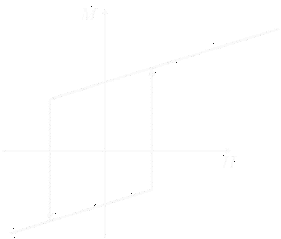

フェリ磁性体・弱強磁性体の典型的な磁化過程

転移点より上,常磁性の場合でも，その磁化過程がBrillouin関数に乗るのであればスピン間の相互作用が ほとんど無く，もしBrillouin関数より上に(つまり弱い磁場でより大きな磁化が出る)ので あれば強磁性的な，逆に下に出るのなら反強磁性的な相互作用が働いているのだと言う事が 分かります．
また，飽和磁化からは(スピンの大きさ×スピンの数)が分かるわけですが，スピンが不純物として 入っているとか，その数が正確にわからない場合があります．そんなときでも，スピン間に 相互作用が無いような系(ナノ粒子で，粒子状に保護分子がついていてナノ粒子間の距離が大きい場合など) だと，Brillouin関数でスピンの大きさを変えていったときの各カーブと比べて，どのスピンの 大きさの時のカーブと一致するかで個々の粒子のスピンの大きさが推測できます． 例えばS=1/2のスピンがN個ある場合と，S=5/2のスピンがN/5個ある場合では飽和磁化は同じですが， 後者のほうが低磁場で飽和するため見分けがつくわけです．

このように，磁化過程は非常に多くの情報を含んでいますので，細かく解析すればするほど スピン構造に関するヒントを手にする事が出来るわけです．