交流磁化率の解析（に限らず，交流回路や誘電緩和などの緩和現象の解析に広く使われていますが） で用いられる手法の一つに，Cole-Coleプロットと呼ばれるものがあります． これはχ'-χ"平面上に各周波数・温度での値をプロットしていくというもので，デバイ型の 単緩和の場合はきれいな半円形のグラフが得られます．これに関して簡単にまとめてみたいと思います．
まず，複素磁化率χ^* = χ'-iχ"は，応答関数Φ(t)と以下の関係で結ばれています．

ここでχ_∞は周波数が無限の極限での磁化率（つまり完全に追従する成分），Lはラプラス変換

を表します．デバイ型の単緩和の場合，応答関数は

で表されますから，これを代入して計算することでデバイの式

が得られます．ここでχ_sは周波数ゼロの極限での磁化率，つまり静磁化率です． このデバイの式で表される複素磁化率の実数部分が測定されるχ'，虚数部分がχ"に対応します． 実際にちょっと計算して実部・虚部にわけ，それぞれを自乗していただくとわかるのですが， このωτを変数とするχ'とχ"の関係式は，χ'-χ"平面における円（半円）になります． ですから，測定したχ'-χ"をプロットし，きれいな半円に乗るようなら，その系は ほぼデバイ型の単緩和で表される緩和機構を持った系であると言っても良いでしょう． 以下に，デバイ型単緩和な場合のCole-Coleプロットおよび交流磁化率の周波数依存を示します．

　　　　

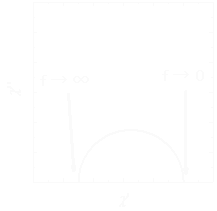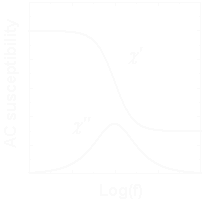
さて，このように単緩和な場合は簡単に表せるのですが，通常の系では緩和が一つ（他の緩和との速度差が大きく実質一つとみなせる） 系ばかりなわけではありません．その場合，緩和時間の異なるいくつかのデバイ型緩和に 重み付けをして足し合わせることで，これらの緩和を表すことが出来るようになります．

この式を用いての解析は，明らかにかなり緩和時間の異なる二つや三つの緩和が存在する場合には何とか行う可能です． しかしながら，実際には緩和時間が近かったり，いくつもの緩和がある程度の幅を持って重なっていたりするため， 容易に緩和過程が分離できずに解析できない事が多々あります． そのような場合には，以下のようなデバイ緩和の式を拡張した式を用いての解析が行われています．

Cole-Cole型緩和

Davidson-Cole型緩和

Havriliak-Negami型緩和

上記の式に対応するCole-Coleプロットの形はここでは載せませんが，容易に計算可能です．
ただしこれらはデバイ型の緩和の式を形式的に拡張したものであり，ある対応するような物理モデル （緩和の分布）がきちんと決まっているわけではありません（形式的には周波数分布から計算できますが）． ですので，これらの式を用いてフィッティングを行い，緩和の分布の広さなどについてある程度言うことは出来ても， それがそのまま実際の緩和時間の分布と一対一で対応するわけではないことには注意が必要です． むしろ実際の解析では，構造等の情報から緩和時間の数や分布などを推定し，そこからCole-Coleプロットが どのような形になるのかを計算，実測にあわせパラメータを振ったり，適宜，基にしたモデルを修正していくなどの 作業を行って解析を進めていくことになります．