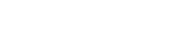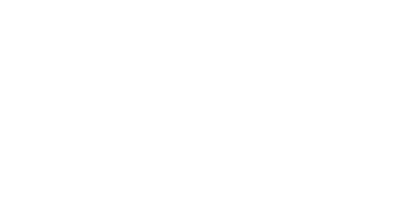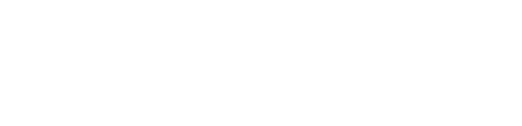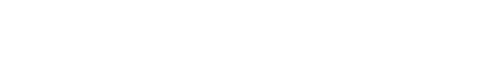|
さて,実際の系では前回述べたような単純な2サイトの系はほとんどなく,事実上無限と
みなせるような多数のスピンが積み重なった系が大多数となります.そのためほとんど
の場合において前回示したような馬鹿正直な計算は出来ないということになりますが,
例外的にごく一部の系(1次元Ising,外場無しの2次元Ising,1次元XY等)に関しては
厳密解が知られています.厳密解が得られる系はごくわずかであるためこれらの解が
直接役に立つことはそう多くはないのですが,なんといっても余計な効果の混入/重要
な現象の排除を心配する必要のない厳密解ですから,「相転移」という現象の本質や
特徴に関する研究に用いられたり,近似法の検証(厳密解の得られている系に近似を
適用し,得られた結果と厳密解を比較する)に用いることができるわけです.
ただ,一般的な系において相互作用の大きさを求めようとする場合にはこれら厳密解
が使えることは少ないため(1次元Isingなどは低次元系で使えることもありますが),
実際には何らかの近似やモデル計算によって得られている式を測定値に対してフィッ
ティングすることが多くなるかと思います.ここでは,それらの中から代表的な
いくつかの例に関して記述したいと思います.
1次元系
・1次元Ising系
ハミルトニアンは
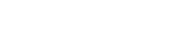
で表され,すべてのスピンはz方向のみの成分±1/2を持ちます.この系の
z方向に磁場をかけた際の磁化等は前述の通り解析的に解くことが可能で,
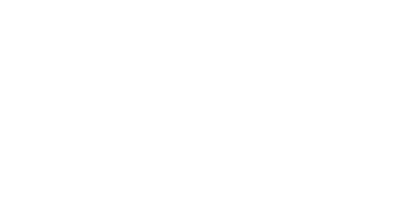
となります.
・1次元Heisenberg反強磁性
Ising模型ではz軸方向しか考えなかったのに対し,Heisenberg模型ではスピンの
xyzの全成分が絡んできます.この系は解析的に解くことはできませんが,
有限系で実際に計算を行い,それを無限系に外挿してフィッティングを施した式が
報告されており,これらを実験結果と比較することで相互作用の大きさを見積もる
ことが可能となっています.計算を行った二人の名前からBonner-Fisher[1]と呼ばれて
いますが,実際にその結果をフィッティングして使いやすく定式化されたものが後に
別のグループにより報告され[2],その式
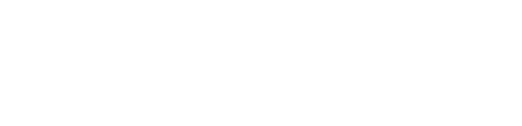
を用いて解析が行われています.ここで相互作用J は前述のハミルトニアンで定義される値とします
(ハミルトニアンの定義の仕方により,スピンの積にかかるprefixが2JなのかJなのか,
という二種類の流儀があり,両者によってフィッティングの式の係数が変わってきます
ので確認が必要です).
同様の手法をS = 1のスピンに適用した[3]
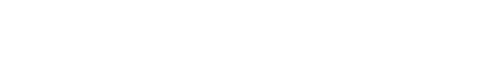
という結果も知られています.ただしこの式にはゼロ磁場分裂(主にスピン-軌道相互作用に
由来する,異方性をもたらす項)の影響が入っていないため,低温においてはこの式よりも
さらにχT の値は減少します.そのためフィッティングをある程度高温側
のみで行うか,まともにゼロ磁場分裂項を取り入れて計算し直してやる必要がある
事には注意が必要です.
・1次元Heisenbergフェリ磁性鎖
同様の計算はフェリ鎖に関しても行われており,例えば[1/2-s](s = 1, 3/2, 2, 5/2)
のフェリ鎖に関して比熱の極大温度やχT の極小温度を求めたものなどがあります[4].
便利に使える式としては,フェリ鎖のχT の値を低温での発散項と高温での
活性化型の項の和として表した
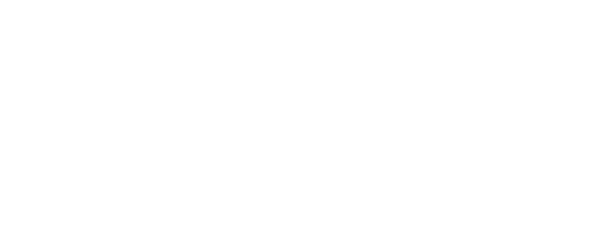
があります[5].細かな議論ができるわけではありませんが,実験値からおおよその
相互作用を見積もることが可能です.
また,1/2-1と1/2-5/2のフェリ鎖の場合での多項式でのフィッティングの結果
も報告されています[6].
・1次元Heisenberg強磁性鎖
S = 1/2 1次元Heisenberg鎖の高温展開法による磁化率の計算結果を多項式に
より表したものが報告されており[7],これを用いて相互作用を見積もることが可能です.
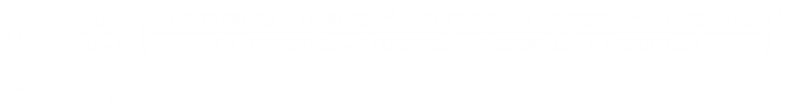
[1] J.C. Bonner and M.E. Fisher, Phys. Rev., 135, A640 (1964).
[2] W.E. Estes et al., Inorg. Chem., 17, 1415 (1978).
[3] A. Meyer et al., Inorg. Chem., 21, 1729 (1982).
[4] M. Drillon et al., Phys. Rev. B, 40, 10992 (1989).
[5] J.S. Miller and M. Drillon, Magnetism: Molecules to Materials vol. I, Wiley-VCH.
[6] Y. Pei et al., Inorg. Chem., 26, 138 (1987).
[7] G.A. Baker Jr. et al., Phys. Rev., 135, A1272 (1964).
|