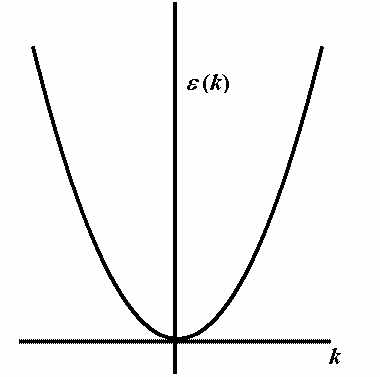
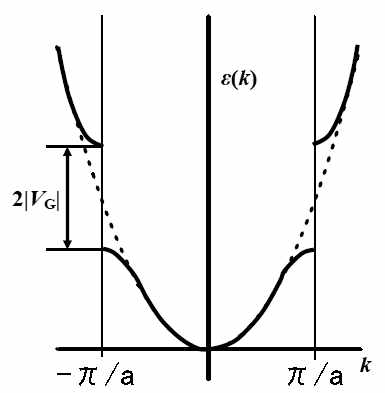
電気伝導は基本的には電子の移動です．そこで通常原子核などはほとんど移動せず 固定されたポテンシャルを作っており，そこを電子が流れていく，という描像が基本となります． さて，そのような描像に基づく伝導の理論展開において，大きく二種類の方法があります． 一方は何も無い空間中を電子が自由に飛びまわるというのを基本とし，そこに原子の作る 弱いポテンシャルが効いているとする自由電子に基づくモデル（これをNearly Free Electronモデル＝NFEモデルと呼びます）， もう一つは電子は基本的に各原子の原子軌道に近い軌道に位置し，隣接する原子軌道間を 飛び移ることで電気が流れる，という側から考えていくモデル（Tight-Bindingモデル）です． まあ両者とも近似を高めていけば一致するわけですが，一般にアルカリ金属やアルカリ土類金属などの 伝導性が良く電子間相互作用の少ない系ではNFEモデルが，分子性導体や重い電子系など 電子が移動しにくく電子間の相互作用が相対的に効いてくるような系では後者を用いた方が 良く現象を説明できることが知られています．まあ，両者の前提を考えればそれも当然のことですが．

さて，ではまずNFEモデルを見ていくとしましょう．まずポテンシャルの全く無い，長さLの 周期的境界条件を持つ系を考えます． この系の電子の状態はポテンシャルの無い単純な1次元Schrödinger方程式を解くだけですから，ψ_k = A exp(ikx )と求まります．ただしここで A は規格化定数，k は波数で2πn/L（nは正負の整数）です． さてこのようにして出来る状態を波数-エネルギー図（これをバンド構造と呼びます）にすると，エネルギーは上記波動関数から 波数の自乗に比例することがわかりますから，単純な二次曲線となります． またLが十分大きい場合，この準位間のエネルギー間隔は非常に狭くなることもわかるかと思います．

さて，次にここにある周期a を持った弱いポテンシャルが加わったと考えます． これは例えば周期的に原子が配列している結晶などで，電子のエネルギーに比べポテンシャルの 寄与が小さい場合が相当します． 波動関数が波数表示でしたので，ポテンシャルもフーリエ変換して波数空間で考えてやるとします． ポテンシャルはa の周期を持っていましたから，波数空間ではこのポテンシャルは k_V = 2mπ/a (m = 0，&±1・・・)の波数へと分解されます．（V→ΣV_k ） 我々の知りたいのは，このポテンシャルの存在下で電子の状態がどう変わるかです． ポテンシャルは弱いわけですから，元の波動関数からは摂動として考えられます． ポテンシャルによる変化は摂動論により元の波動関数でポテンシャルを挟んだもの Σψ_k'・V・ψ_k で与えられます． またポテンシャルは2mπ/aの波数成分のみ持つため，上記の項が値を持つには k k とk' の差が2mπ/a の時のみになります． さらに，摂動によって状態が十分混じるには混ざる二つの状態のエネルギーが非常に近くないと いけませんので，混合するのは

・波数の差が2mπ/a
・エネルギーがほぼ等しい

という状態間になります．

さてここで完全に自由な電子の波動関数に戻ります．ここでは状態は波数に対してほぼ連続で， そのエネルギーは波数の自乗に比例すると書きました． ということは，軌道間の混合条件を満たすのは波数k に対し-k でかつ その差k -(-k ) = 2k が2mπ/a となるものだけです． 詳しい計算（このへんの参考書を参照のこと）は省きますが， 状態二つが混じるとエネルギーの低い状態と高い状態の二つに分裂します．そのためバンド構造は 下図のように変わり，波数±nπ/a でエネルギーに飛び（バンドギャップと呼ばれます） が生じてきます． これにより，結晶中の電子はある範囲のエネルギーをとることが出来なくなります．

図に示した弱いポテンシャル中のバンド構造，ここで書かれているのは上と下の二つのバンドです． さて，波数k が正の領域の電子は右向きの運動量を持っています． 一方，波数が負の電子は左向きの運動量を持つわけです． 電場がかかっていないときは電子は当然低い順位から波数の正負を問わず状態を埋めていきますから， 右に行く電子も左に行く電子も同数，つまり電流はありません． ここに電場を書けると，電子が加速され状態分布が変わります．これにより波数正の電子と負の電子の 数が等しくなくなり，電流が現れるわけです． さて，ここで図中の下側のバンドが完全に埋まった状態を考えましょう．これはフェルミエネルギー （電子の化学ポテンシャル）がバンドギャップ中にある場合に相当します． この場合，電子の波数分布を不均一にするには，電子にバンドギャップの上へ上がる分のエネルギーを 与えてやらねばなりません．そのため，かなりの電場をかけねば波数正の電子と負の電子は 同数のままであり，電流が流れません．これが絶縁体と呼ばれる物質群となります． ただ実際には上のバンドへ熱励起されている電子が存在するため，そのような電子が 少しは電子を流します． バンドギャップが小さければ小さいほど（エネルギー差が小さいため）熱励起された電子の数も多くなります． このようなギャップの小さい絶縁体のことを（真性）半導体と呼んでいます． 温度が高いほど同様に励起された電子の数は多くなりますから，半導体では温度の低下とともに 抵抗が上昇していきます．

一方，金属の場合はバンドの途中にフェルミエネルギーがあるため，容易に電子の波数分布を 非対称にすることが出来ます．このため電場をかけるとすぐ電子が流れ，低い抵抗を示します． 金属では電流を担うのは熱励起された電子ではなくもともと存在するバンド中の電子なので， 温度を上げたからといって伝導を担う電子数は増えず，むしろ格子振動による散乱が増えるため 半導体とは逆に温度の上昇とともに抵抗が上昇します． 伝導にはさまざまな効果が関与するため例外もありますが，基本的には温度の上昇とともに 抵抗が下がるのが半導体，上がるのが金属です．