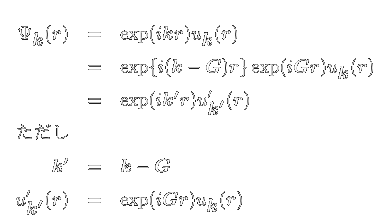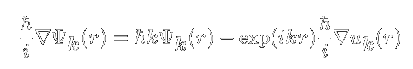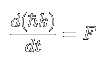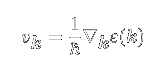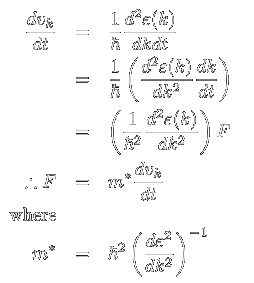|
伝導関係を扱っている人はよくバンド構造の図などを書くわけですが,他の分野の方からはこれが 非常にわかりにくいと言う言葉をよく聞きます.そこでここでは,バンド構造などはどういった ものなのかということを簡単に書いてみたいと思います. 波数
さて,そもそもバンド構造というのは,波数を変数にした時に,ある点(=波数)を持つ電子が
どんなエネルギーを持っているのか,を示すものです.ではここで言う波数とはどんなもの
なのかを簡単に書いてみたいと思います.
とあらわされます.ここでuk(r)はポテンシャルと同じ周期Rをもつ 関数であり,Rの並進に対し, Uk(r+R)=Uk(r)となります. この物理的意味は以下のように考えられます.結晶中のある点の状況は,その点を結晶格子の 整数個分だけずらした点の状況と全く同じです.そのため直観的に,両方の点の周囲において 電子の波動関数は同じ形状となっていおり,物理量は格子定数倍ずれたところでも一致すると 考えるのは自然なことです. 一方,波動関数の位相そのものは物理的意味を持ちませんから,格子定数倍ずれた点で位相が 異なっていたとしても,物理的な値は変わりません.ただし,位相そのものは物理的に意味を もたないと言っても,位相差は意味を持ちます.ですから,ある点AからL=nR移動した際に ずれる位相は,A+Rという(点Aから格子の整数倍ずれた)点から同じだけ移動した際にずれる 位相と,完全に同じでなくてはいけません. そうでなければ,まったく同じポテンシャルが周期的に続いているのに,ある点とそこから ポテンシャルの周期の整数倍だけずれた物理的に区別のつかない別の点とで波動関数の様子が 異なるという妙なことになってしまいます. では,このときの波数(の絶対値|k|)の最低値,最高値はいくつになるのでしょうか? 最低値は簡単で,となりの格子に移動しても全く位相のずれが無い波数k=0です. では最高値は?Blochの定理で出てくるexp(ikr)を考えると,いくらでも大きな 波数が考えられそうです.そういう立場から,|k|の上限を考えずにどんどん大きなkをとって, その状態でのエネルギーを考えてバンド構造を書いてやるというのが一つの書き方で, 拡張ゾーン形式と呼ばれます.
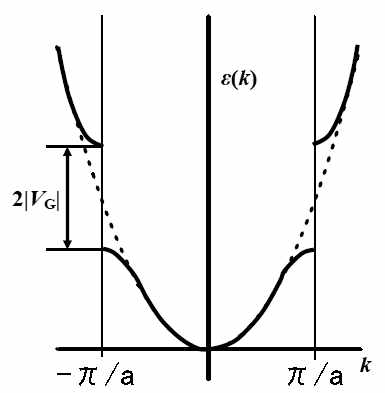
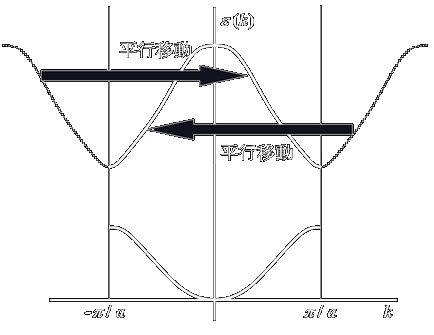
拡張ゾーン形式 一方,波数kが±π/a(ここで1/aは逆格子)よりも外に位置する 場合,以下に示すように波数に対し逆格子ベクトルGの整数倍を足したり引いたりする ことで±π/a内の波数範囲(第一ブリルアンゾーン)の関数へと平行移動 して考えることが可能です.(∵exp(iGr)もuk(r)と同じく Rの並進に対して不変であり,以下のような変形を行ってもBlochの定理を破らないため)
こうやって波数を±π/aの第一ブリルアンゾーン内に還元してやった 表記を還元ゾーン形式と呼びます.
還元ゾーン形式 このようにすると,波数をある範囲内で考えることができます.さらに後に述べるように 結晶中の電子は逆格子に相当する波数を結晶格子とやり取りすることにより波数を変化させる ことが可能であり,k,k±G,k±2G…の波数の間で比較的簡単に移り変われる わけですが,それがこの図では波数軸方向への移動のない,垂直遷移に対応します. つまり,結晶中の電子が他の粒子などとの間で運動量をやり取りしない励起などは,この図中 では(通常の空間での場合の運動量をやり取りしない遷移と同じように)垂直の遷移で 表わされるわけで,理解がしやすくなります.
波数の物理的意味さて,ここで結晶中の電子の波動関数に対し運動量演算子を作用させると
となります.ポテンシャルが存在しない場合(=自由電子の場合)は第二項が消えて,この関数は 運動量の固有関数となり,固有値(=運動量)ħkを持ちます.一方,結晶中ではポテン シャルの存在により第二項が現れ運動量の固有関数ではなくなりますが,これは結晶では周期的な ポテンシャルの存在により並進対称性が消失していることに関係します. 「作用が,ある連続変換に対し不変である時(系がある対称性を持つ時),必ずそれに付随した 保存量が存在する」という大変強くまた美しいNoetherの定理というものが存在します. 例えば系が時間方向への並進でも変化しない(閉じた系で物理法則が時間に依存しない場合など) は保存量としてエネルギーが現れますし,並進対称性が存在する(位置によらず物理法則が同じ) 時には運動量が,回転対称性が存在する(どちらの方向でも物理法則は同じ)場合には角運動が 保存され,ゲージ変換不変性から電荷の保存が導かれます.これらわかりやすい対称性だけでは なく,いくつかの力学変数などを組み合わせたその物理的意味がわかりにくいものに関する 対称性を持つ場合などもありますが,その場合でも対応する保存量が生じます. このように,結晶中の電子の運動量を考えると余計な項がついていて面倒に思えますが,実際の 散乱過程や,電場・磁場への応答を考える場合,ħkが運動量である,として話を 進める事が可能です.電場や磁場は電子のħkの値を変え,その運動に変化を もたらします.詳細は省きますが,電子に働く力Fと,電子の波数kとの間には
という関係が成り立ちます.これは,ħkを運動量とみなせば,運動量の変化分は
加えられた力に等しいという,古典力学での描像そのものです.
という保存則が成り立ちます.ここでGは逆格子ベクトルで,散乱などの際に逆格子 ベクトルに相当する分の運動量を結晶格子系が吸収/放出可能であることに由来します. これも,結晶に吸収される分を除けば,運動量保存則に相当するものとなります. 例えば,空間中に固定された障壁があった場合並進対称性は失われますから,その対称性に付随 した保存量であるところの運動量ももはや保存量ではありません.これは例えばボールを(空間 中に固定された)壁にぶつけると,ボールが跳ね返る(=運動量が保存されていない)事に対応 します.もちろん,実際には壁を空間中に完全に固定することはできず,(ボールを見ている 範囲では)保存されなかった運動量の差は壁に吸収されているわけですが. (結晶格子を空間中に固定されたとみなす系で考える)結晶中の電子でもこれと同じ事が生じ ます.電子の運動量は,その一部を結晶格子に渡す(結晶格子から受け取る)事で変化すること が可能です.しかしながら結晶格子はある周期での並進に対して不変という(単なる空間での 連続並進に対する対称性とはちょっと違いますが)対称性を持つため,単純な運動量保存則とは 違うもののある種の保存量が出てきます.この通常の運動量保存則とのずれに相当する分が結晶 によって持ち去られる/与えられる運動量Gとなります.
有効質量再び細かい話は抜きにしますが,波数k周辺の波で構成される波束の平均速度は,
と,エネルギーを波数で微分したものとしてあらわされます.まあ波束ではなく, ある波数kの電子の平均速度と思っていても通常はそれほど外れてはいません. とは言え波数kの電子は結晶全体に広がっている状態ですので,その速度というと ちょっと変なことになりますが. これを時間で微分し,上の方で出てきた外力と波数の時間変化の関係を用いると
と,あたかも電子がm*の質量をもった粒子として外場に応答しているかのように 扱えることがわかります.
具体例を示しましょう.上の方に示したバンド構造の模式図で一番下のバンド(途中で切れた放物線
のようなもの)に注目すると,バンドの底(k=0)付近ではバンドの傾きはゼロ,二次微分は
正ですから,このあたりの波束は速度がゼロで,ある質量をもって外場に応答する粒子として
扱えます. 速度がバンドの傾きに対応し,外場は波数を増やす,という二点に注目して,同じ様子を見てみます. まず原点付近では,外場によって波数が増えるとバンドの傾きは増します.つまり,外場で 速度が増えるわけです. 一方中間付近では,波数が増えても傾きの変わらない点が存在します.ここでは,外場によって 波数は増えるものの,それが速度の増加と結びついていないわけです. 最後にバンドの端近くでは,波数が増加するとバンドの傾きは逆に小さくなってしまっています. ですから,外場によって波数が増えると速度が落ちるわけです. もちろん,実際の電子の質量が無限大になったり負になったりしているわけではありません. バンドの端近くでは,ポテンシャルの存在により,自由電子で言うところの波数kの状態と, 逆側にいる波数k-G(≒-k)の状態がだんだん混ざってきているということを思い出す必要があります. バンドの端に近づけば近づくほど,正反対の波数を持つ成分=逆向きの速度を持つ成分が 混じってきて,結果として速度が遅くなってしまっているのです. これは,波束が結晶の周期的ポテンシャルでブラッグ反射されて,逆向きに進む波が生じて 混じってきている,とみなすことも可能です. その反射の過程において,本来電子が受け取るはずだった運動量は結晶格子に受け渡され, 「電場で加速するほど遅くなる」という一見不合理な結果をもたらすわけです. このように,結晶中の電子の運動を考える際は,(背景として一旦思考の外に追いやった) 格子の存在とその影響が本来無視できません.バンド構造で捉えるということは,その格子の 存在をとりあえず追いやって,その効果をすべて「バンド」の構造に押し込めている, というわけです. |