電気伝導度を測定しようと思った場合，一番基本となるのは直流での2端子法と4端子法です． それぞれのセッティングおよび等価回路図を下図に示します．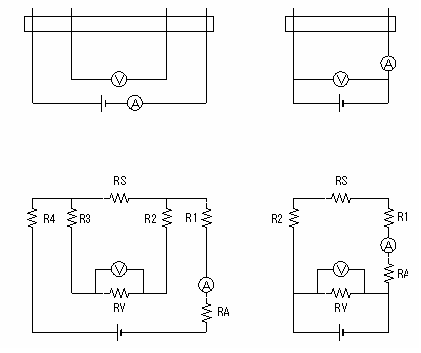

図の左側が4端子法，右が2端子法で，それぞれ上段が接続図，下段が等価回路となります． 図中R1-R4はサンプルとリード線との間の接触抵抗（リード線そのものの抵抗も含む），RSが サンプル抵抗で，RV，RAはそれぞれ電圧計，電流計の内部抵抗となります． 接触抵抗はサンプルとの接合に依存するので具体的な値は不明ですが，おおよそ0〜100Ω 程度のオーダーであることが多いと思います．電圧計の内部抵抗は（レンジによっても 異なりますが）1〜10GΩ程度，電流計の内部抵抗は（こちらもレンジによって異 なりますが）1〜10Ω程度とおおよそ考えられます．

まず4端子法に付いて考えてみます．接触抵抗R2，R3はRVに比べ無視できるほど小さいので， これらの影響は考えなくとも良くなります． またR1，R4がいくつであろうとも，サンプルにかかっている電圧を電圧計で読む際には 影響しませんのでこちらも無視できます．加えてRAもサンプルに流れる電流値，そこにかかっている 電圧の電圧計による読みには影響を与えませんので無視します． そうすると4端子法の場合の回路図は下図のように簡単なものとなります．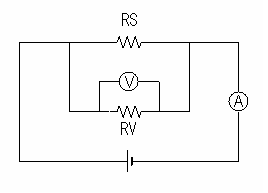

こうなると問題になるのはRSとRVの関係だけです．RSがRVに比べ十分小さいときはRVを 流れる電流は無視できますから，測定値は正しい抵抗を与えます． 一方，電圧計の内部抵抗に対しRSが無視できない大きさにまで大きくなったときは， 電圧計内部を流れる電流まで一緒に電流計で測定してしまいますので，サンプル抵抗を 低く見積もってしまうことになります． RVが1GΩとすると，誤差が1％程度になるのはサンプル抵抗が10MΩ程度の ときですから，これ以上の抵抗のサンプルの場合は4端子法は向いていないと言えます．

*現実的には，数十kΩ以上のサンプルの場合は2端子法が向いているのではないかと思います．

一方の2端子法ですが，電流計での測定値に対するRVの寄与は無視できます． そして，サンプルの抵抗が接触抵抗や電流計の内部抵抗に比べ十分大きい場合にのみ， これらの余計な抵抗の寄与が無視できます． そのため，サンプル抵抗が数百kΩ以上の場合には2端子法で十分正確な測定が出来ると考えられます．

以上から，抵抗が0〜数十kΩまでは4端子法で測定し，それ以上になってきたら 2端子法に切り替える，と言うのが直流抵抗測定での基本となります．